1-41-2: 平行でない３力のつり合い ＜例題＞

例題　

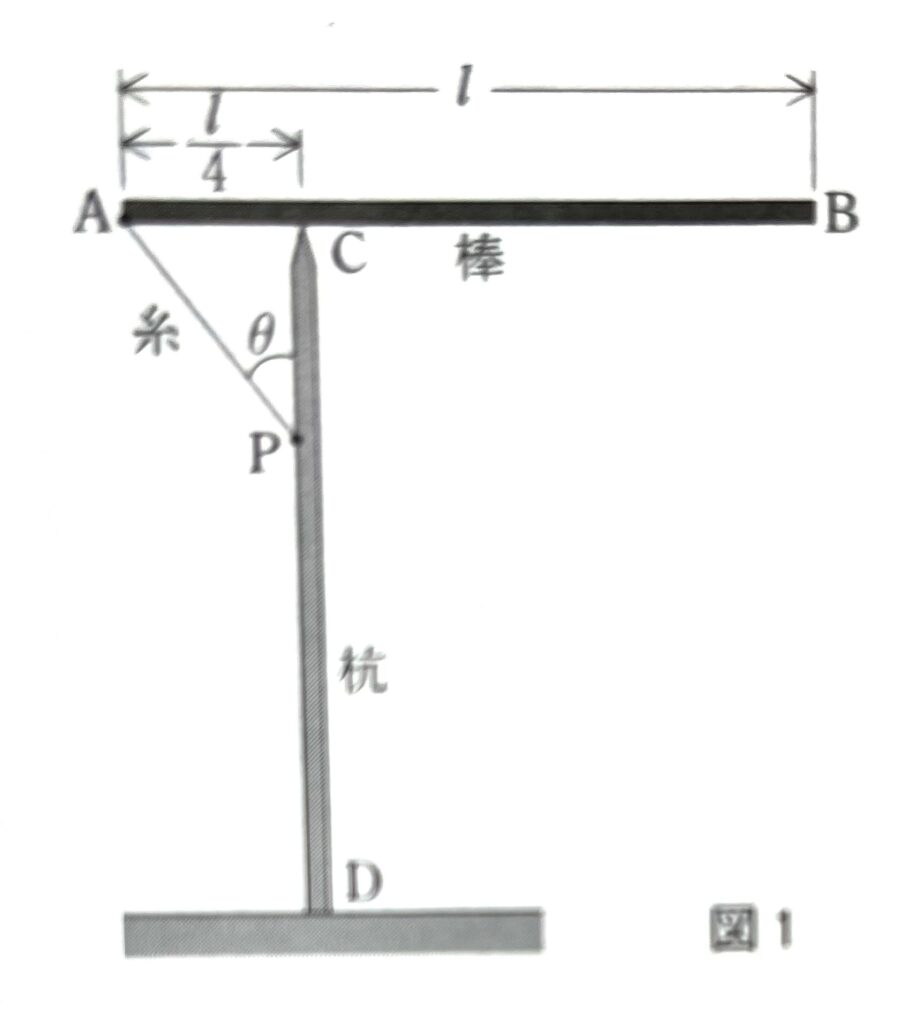
　図１のように、長さ\(l\)の一様な棒ABの端Aに糸を結び、この糸の他端を鉛直に立てた杭CD上の点Pにつなぎ、棒を杭の上に置いたところ、棒は水平になり静止した。このとき棒が杭と接する点Cは点Aから距離\(\displaystyle \frac{l}{4}\)にあり、糸が杭となす角度は\(\theta\)であった。

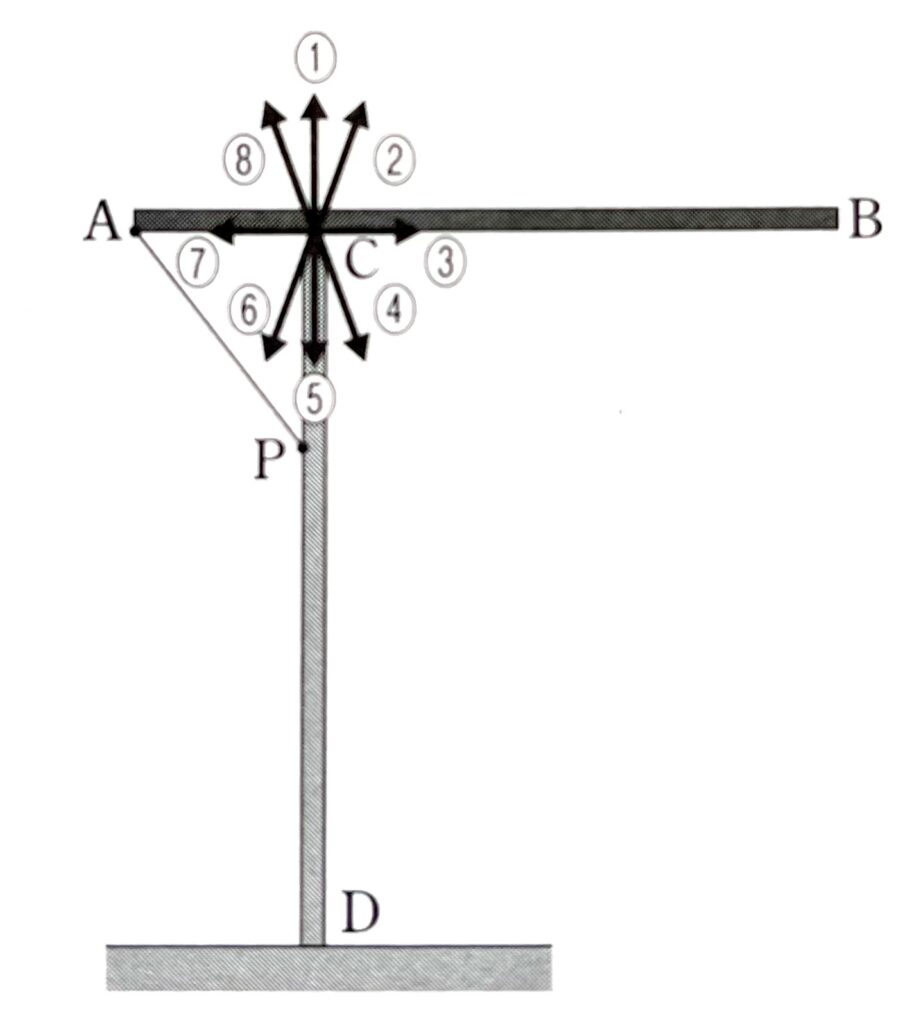
問１　点Cで杭が棒に及ぼす力の方向として最も適当なものを、図２の①～⑧のうちから一つ選べ。

問２　棒ABの質量を\(M\)とするとき、糸の張力\(T\)はいくらか。正しいものを、次の①～⑥のうちから一つ選べ。ただし、重力加速度の大きさを\(g\)とする。
①　\(\displaystyle \frac{Mg}{2\cos\theta}\)　②　\(\displaystyle \frac{Mg}{2\sin\theta}\)　③　\(\displaystyle \frac{Mg}{\cos\theta}\)　④　\(\displaystyle \frac{Mg}{\sin\theta}\)　⑤　\(2Mg\cos\theta\)　⑥　\(2Mg\sin\theta\)

解答・解説

問１　棒に働く力を聞かれているので、棒を注目物体にする。棒に働く張力\(T\)は書くが、杭に働く張力は書かない。1-41-1の通り「平行でない３力のつり合いでは、作用線が１点で交わる」から、④か⑧が正解。
　\(T\)は水平右向き成分を持つので、水平方向の力のつり合いが成り立つためには、\(f\)が水平左向き成分を持たないといけない。よって図３の通りになる。　　　　答　⑧

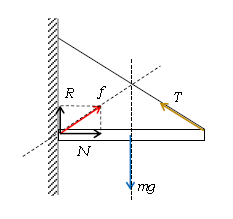
＜補足＞　杭の先端を、簡単のため狭い水平面のように捉えよう。面から働く力は垂直抗力\(N\)と摩擦力\(R\)の２種類（図４）で、ここでの\(f\)はまさに\(N\)と\(R\)の合力。

　例えば、図５でつり合いが成り立つときの３力\(f,T,mg\) の向きは、作用線が１点で交わるから図の通り。このときの壁から棒に働く力\(f\)も、\(N\)と\(R\)の合力である。
　問題文に「なめらかな壁」とない限り、\(N\)だけでなく摩擦力\(R\) も考えなければいけないから注意しよう。

問２ 図６a の張力\(T\)のように力の向きと回転半径が垂直でない場合、モーメントの向きが左回りなのか右回りなのか分かりづらいというのであれば、図６ｂのようにする。力を作用線に沿って動かして垂線(うで)の足の所まで持ってくる。その上でモーメントの中心（杭の先端）を（頭の中で）ピン止めして張力\(T\)で引っ張ってみる。すると\(T\)のモーメントは左回り(反時計回り)だと簡単に分かる。

　モーメントのつり合い　\(\displaystyle 0=T\cdot\frac{l}{4}\cos\theta-Mg\frac{l}{4}\)
　∴　\(\displaystyle T=\frac{Mg}{\cos\theta}\)　　　　答　③