1-10-2: 親ガメ子ガメ <例題>
有名な「親ガメ子ガメ」の問題を練習しましょう!
例題
図のように、水平な床の上に質量\(M\)の直方体の台があり、その上に質量\(m\)の小物体がのっている。台を右向きに大きさ\(F\)の力\(F\)で引っ張ったところ、台は動き出して、小物体は台上を滑りだした。以下では加速度の正の向きを右向きとし、重力加速度の大きさを\(g\)とする。
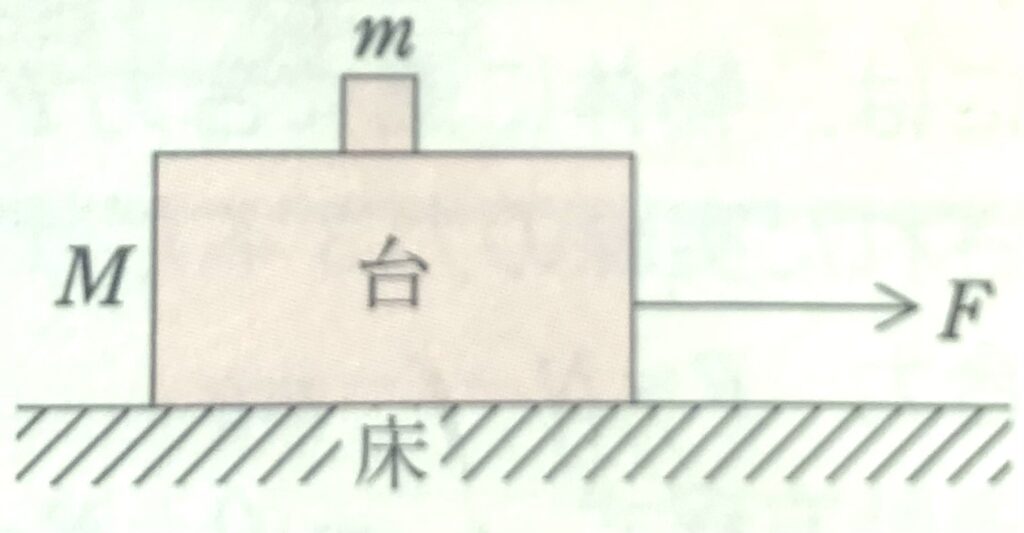
問1 台と小物体の間に摩擦はなく、台と床の間の動摩擦係数を\(\mu\)とする。このときの台の加速度はいくらか。正しいものを、次の①~⑧のうちから一つ選べ。
① \(\displaystyle \frac{F+\mu mg}{M} \) ② \(\displaystyle \frac{F+\mu mg}{M+m} \) ③ \(\displaystyle \frac{F-\mu mg}{M} \)
④ \(\displaystyle \frac{F-\mu mg}{M+m} \) ⑤ \(\displaystyle \frac{F+\mu (m+M)g}{M} \)
⑥ \(\displaystyle \frac{F+\mu (m+M)g}{M+m} \) ⑦ \(\displaystyle \frac{F-\mu (m+M)g}{M} \)
⑧ \(\displaystyle \frac{F-\mu (m+M)g}{M+m} \)
問2 台と床の間に摩擦はなく、台と小物体の間の動摩擦係数を\(\mu\)とする。このときの台の加速度と小物体の加速度はそれぞれいくらか。正しいものを、次の①~⑥のうちから一つ選べ。
① \(\displaystyle \frac{F}{m} \) ② \(\mu g\) ③ \(\displaystyle \frac{F-\mu mg}{M} \) ④ \(\displaystyle \frac{F+\mu mg}{M} \)
⑤ \(\displaystyle \frac{F-\mu mg}{M+m} \) ⑥ \(\displaystyle \frac{F+\mu mg}{M+m} \)
解答・解説
1-08-1: 力学攻略の基本 の流れに従って行く。
問1 まず軸と力 図1、2。
図1は鉛直方向の力(わざと2物体を離して書くと、図が見やすい)。注目2物体がふれ合っている所での作用反作用に注意(1-10-1)。
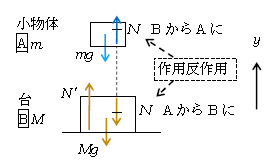
図2は水平方向の力。
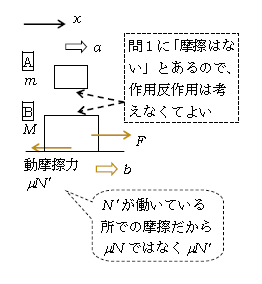
次に\(ma=F\) A、Bの加速度をそれぞれ\(a\)、\(b\)と図示した(図2)。
図1 A: \(0=N-mg \) (\(m0=N-mg\)という意味) (1)
図1 B: \(0=N’-N-Mg \; \) (2)
図2 A: \(ma=0 \;\, \) (3)
図2 B: \(Mb=F-\mu N’ \, \) (4)
(1)より \(N=mg \; \) (5)
(2)に代入 \(N’=(m+M)g \) (6)
(4)に代入 \(Mb=F-\mu (m+M)g \)
∴ \(\displaystyle b=\frac{F-\mu (m+M)g}{M} \) 答 ⑦
問2 まず軸と力 鉛直方向の力は図1と同じだから、再び(1)(2)が成り立って(5)(6)が使える。水平方向だけ調べよう。
さて、この台と小物体タイプを「親ガメ子ガメ」というが、親ガメの方を引くときの摩擦力の向きは、次のように考える ―― そもそも接触面(親ガメと子ガメの触れ合っている面)どうしはくっついていたがる性質があり、だからこそすべるのを妨げる摩擦力が働く。いま力\(F\)で右に引かれて親ガメが右へ加速しようとすると、子ガメは親ガメにくっついていたがり右へ加速しようとする。つまり、「親ガメから子ガメに」いわばついてこいと命令をかける形で摩擦\(\mu N \)が右向きに働く(図3中の青色矢印)。すると作用反作用により「子ガメから親ガメに」摩擦\(\mu N \)が左向きに働く(黄色の矢印)。
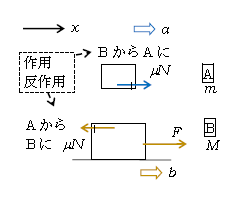
次に\(ma=F\)
\(x\)方向の運動方程式 A: \(ma=\mu N \; \) (7)
\(x\)方向の運動方程式 B: \(Mb=F-\mu N \) (8)
(5)を(8)に代入して \(Mb=F-\mu mg\)
∴ \(\displaystyle b=\frac{F-\mu mg}{M} \) 台 答 ③
(5)を(7)に代入して \(ma=\mu mg\)
∴ \(\displaystyle a=\mu g \) 小物体 答 ②


