6-01-2: エレクトロンボルト(eV)

エレクトロンボルト(eV)は原子物理でしばしば用いられるエネルギーの単位です。　　　

※　ページ最上部の（一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから）各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。

　まずは1eVの解説に必要な実験状況の説明から。
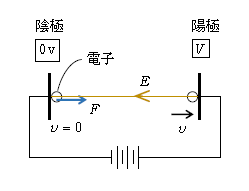
　原子物理では、電子や陽子といった荷電粒子にエネルギーを与えて加速し、それを別の微粒子(電子、原子核、原子分子など)にぶつけて起こる反応を調べるといったことが行われる。荷電粒子にエネルギーを与えるシンプルな方法は、電極間に電圧をかけて生じる電場で荷電粒子を加速するというもの（図１）。
　図１で陰極(電子の出射側)の電位を0Vとし、電源を通してつながれた陽極の電位を\(V\)(>0)[V]とおく。つまり電極間の電位「差」(電圧)は\(V\)。電位の高い陽極から低い陰極へと向く電場\(E\)が生じている。電子の電荷の絶対値を電気素量\(e\)といい、e=1.6×10\(^{-19}\)Cは覚えておくのがよい。電子は負電荷だからその電気量は\(q=-e\)で、電場\(E\)と逆向きに電気力\(F=|q|E=eE\)を受けて陽極へ向け加速する。電位\(\phi \)の下で電荷\(q\)の持つ電気力による位置エネルギー\(U\)は\(U=q\phi =-e\phi \) 。電子の質量を\(m\)、速さを\(v\)としてエネルギー保存則は
　\(\displaystyle \frac{m}{2} v^2+U \)＝一定　つまり　\(\displaystyle \frac{m}{2} v^2+(-e)\phi \)＝一定
となる。図１では
　\(\displaystyle \frac{m}{2} 0^2+(-e)0 \text{ v}=\frac{m}{2} v^2+(-e)V \)　　∴　\(\displaystyle \frac{m}{2} v^2=eV \)　　(1)

　この式の意味は ―― 重力による位置エネルギー\(mgh\)が重力のする仕事=\(mg\)×移動距離\(h\) を表しているように、電気力による位置エネルギー\(eV\)は電気力のする仕事を表し、その仕事の分だけ運動エネルギー\(\frac{m}{2} v^2 \)が増えたということである。
　さて、1eVとは加速電圧1Vで電子の得る運動エネルギーに等しい。加速電圧\(V\)=1Vを(1)に代入すると
　\(\frac{m}{2} v^2=e \)×1V=1.6×10\(^{-19}\)C×1V=1.6×10\(^{-19}\)J
これが1eVで、J 単位の数値部分が電気素量と一致している。\(V\)=10Vにとると、
　\(\frac{m}{2} v^2=e \)×10V=10×1.6×10\(^{-19}\)J 　となり、これは10eV。
つまり、eVとは、加速電圧の数値がそのままエネルギーの数値となるように選んだエネルギーの単位なのである。
　なぜそのような単位を採用するのかの理由は２つ。
　第１に、物理の実験に携わっている研究者からすると、今自分がどの位の電圧で実験中なのか(100Vなのか10000Vなのか）は「肌感覚」としてつかみやすいということ。第2に、原子物理はそもそも非常に小さいエネルギー、例えば1.6×10\(^{-16}\)J などを扱う分野なので、それを1.6×10\(^{-16}\)J と表現するよりも、1000eVと表現する方が好都合だということである。
　後に扱うX線の物理はkeV(けいいーう”ぃーと読む)=10\(^3\)eVが多用され、原子核の物理はMeV(えむいーう”ぃー)=10\(^6\)eVが多用される分野である。ちなみエネルギー世界最大の粒子加速器は10TeV=10\(^{13}\)eVより大きなエネルギーを扱うことがある。