2-08-1: うなり
重ね合わせの原理で生じる現象の第2弾 ―― 振動数の異なる2つの波で「うなり」
※ ページ最上部の(一部スマホでは右上または下側の \(\equiv\) 印「メニュー」をまずクリックしてから)各分野のタイトルをクリックすると、 目次 が見れます。また、スマホは画面を横長にして見ることをおすすめします。
ポイント
・ 振動数\(f_1,f_2\)の2つの波が重なり合って生じるうなりの振動数
(1sあたりのうなりの回数)=2つの音の振動数の差=\(|f_1-f_2| \)
重ね合わせの原理に基づいて起こる現象の第2として、うなり ―― 振動数の非常に近い2つの音波が重なり合うと、音の強弱が周期的にくり返される現象 ―― がある。
例えば振動数442Hzのおんさと440Hzのおんさを同時に鳴らす(図1)と、音が強弱、強弱、強弱、・・・と繰り返して「ウォァン、ウォァン、ウォァン、・・・ 」のように聞こえる。この強弱(ウォァン)1回をうなり1回といい、1sあたりのうなりの回数は、振動数の差442-440=2Hz つまり2回に等しくなる。
そうなる理由を\(f_1\)=10Hzと\(f_2\)=8Hzの2つの音で考えてみよう。(人間に聞こえる音(可聴音)の振動数は20~20000Hz程度だから、10Hz、8Hzでは実際には聞こえないのだが、簡単のためにそれらを考えることにする。)
図2に\(y\)-\(t\)グラフがある。\(y\)-\(x\)グラフではない。2-02-1でやった通り、\(y\)-\(t\)グラフは振動グラフ、ここでは耳元の空気の振動を表す。音1音2ともに振幅\(A\)として、\(f_1\)=10Hzの音1は1s間に(初めを除いて)10回山となり、\(f_2\)=8Hzの音2は8回山となることを、グラフで確認しよう。
初め横軸の左端\(t=0\)では、音1の山○(変位(高さ)\(A\))と音2の山□(変位\(A\))が重なり、合成波は強音●(変位\(2A\))である(合成波の振幅の大きい付近が強音となって聞こえる)。
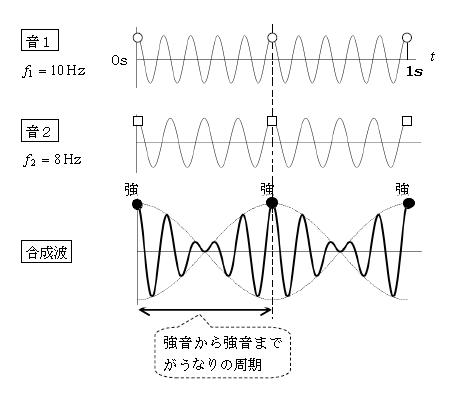
音1と音2の振動回数は異なるから、時間が経つにつれて(横軸の左端\(t=0\)から右の方へ行くにつれて)音1と音2の山の位置は少しずつずれてくる。合成波は強音ではなくなる。
やがて音1と音2の山の数がちょうど1個ずれると(グラフの点線0.5sのときで、このときまで音1は(初めを除いて)山5個、音2は山4個)、再び山○と山□が重なって強音●となる。強音●から強音●までとは、(初めを除いて)弱強1回、つまりうなり1回に他ならないから、2つの音の山の数が1個ずれるたびごとにうなりが1回聞こえることが分かる。
よって1sあたりのうなりの回数は、1sあたり2つの音の山の数が何個ずれるかに等しい。すなわち2つの音の1sあたりの山の数の差――振動数の差――に等しい、というわけである。なお、ここでは\(f_1-f_2\)=10-8=2Hz。確かにグラフより、強音から強音までは1sあたり2回、つまりうなり2回である。


