1-34-2: 束縛条件(張力続き)

1-34-1に続いて、難易度の高めな問題にチャレンジしましょう！　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　単元1-34-1に引き続いて、張力を及ぼすもの(糸・ひも・綱・ロープなど)を全て「糸」という語で表す。図１はおもりA,B,CがあってBが動滑車につながれている状況。A,B,Cの質量が例えば文字でそれぞれ\(m,M,2m\)と与えれているときなどは、下降するのはどのおもりで上昇するのはどれかは分からない。そこで便宜上、下向きを正とする\(x\)軸を取り、正の向きに\(a,b,c\)とおく(図示する)。例えば\(a\)が負の値で求まったなら、実際は上向きに加速するという意味で、決して下向きに加速中という意味ではない。
　糸の長さが一定であることに伴う束縛条件(加速度の関係式)を、1-34-1では動滑車上の観測者から見た相対加速度を考慮することによって求めた。それが簡単だからである。ところが図１のような場合、動滑車上の観測者から見ても一向に見通しがよくはならない。こういう場合は本格的なやり方でやる（が、それはある意味でとっつきづらい方法でもあるので、ここはひと頑張りしてもらいたい）。

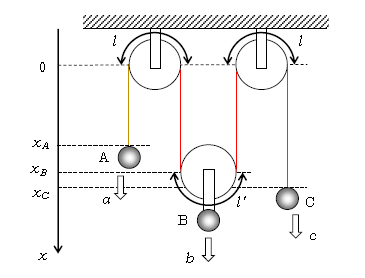
　図１には座標が書かれている。動くおもりA,動滑車B,おもりCの座標はそれぞれ変数\(x_A,x_B,x_C\)で、天井につながれた２つの定滑車(ともにサイズが等しいとする)の座標は動かない定数だから原点0で設定してある。さらに定滑車と動滑車の半円周の長さをそれぞれ\(l,l’\)としてある。ここで糸全体の長さ\(L\)を座標で表してみよう。黄色を付けた糸の長さは\(x_A-0=x_A\)、同様に赤、青を付けた糸の長さはそれぞれ\(2×x_B,x_C\)。あとは滑車の半円周部分の糸の長さ\(2l+l’\)を付け加えて
　\(L=2l+l’+x_A+2x_B+x_C \)　　　　　
　この両辺を時間\(t\)で微分してみる。　[ なぜか。こうするとゆくゆくは上手く行くから微分するので、なぜ微分？と手を止めたりせず、話に付いてくることが大切 ]
　\(\displaystyle \frac{dL}{dt}= \frac{d(2l+l’)}{dt}+ \frac{dx_A}{dt}+2\frac{dx_B}{dt}+ \frac{dx_C}{dt}\)　　　　(1)
　ここで糸の長さ\(L\)は一定(定数)で、定数の微分は0だから \(\displaystyle \frac{dL}{dt}=0 \)
　滑車の半円周部分\(2l+l’\)も定数だから \(\displaystyle \frac{d(2l+l’)}{dt}=0 \)
　\(x_A\)の微分は速度だから \(\displaystyle \frac{dx_A}{dt}=v_A \) と表せる。同様に \(\displaystyle \frac{dx_B}{dt}=v_B \, , \, \frac{dx_C}{dt}=v_C \) 。すると(1)は
　\(0=0+v_A+2v_B+v_C \)
　この式は、糸の長さ\(L\)をそれが定数であることを加味して微分して得られたものだから、まさに糸の長さが一定であることからくる速度の関係式である。この式をさらに\(t\)で微分する。
　\(\displaystyle 0=\frac{dv_A}{dt}+2\frac{dv_B}{dt}+ \frac{dv_C}{dt}\)
　速度\(v_A,v_B,v_C \)の微分はそれぞれ加速度\(a,b,c \)だから
　\(0=a+2b+c \)
　これこそ糸の長さが一定であることに伴う束縛条件である。

　まとめると、動滑車上の観測者から見ても見通しが悪いような場合は、ポイントにある通り、
　糸の長さを座標で表して\(t\)で２回微分するとよい。